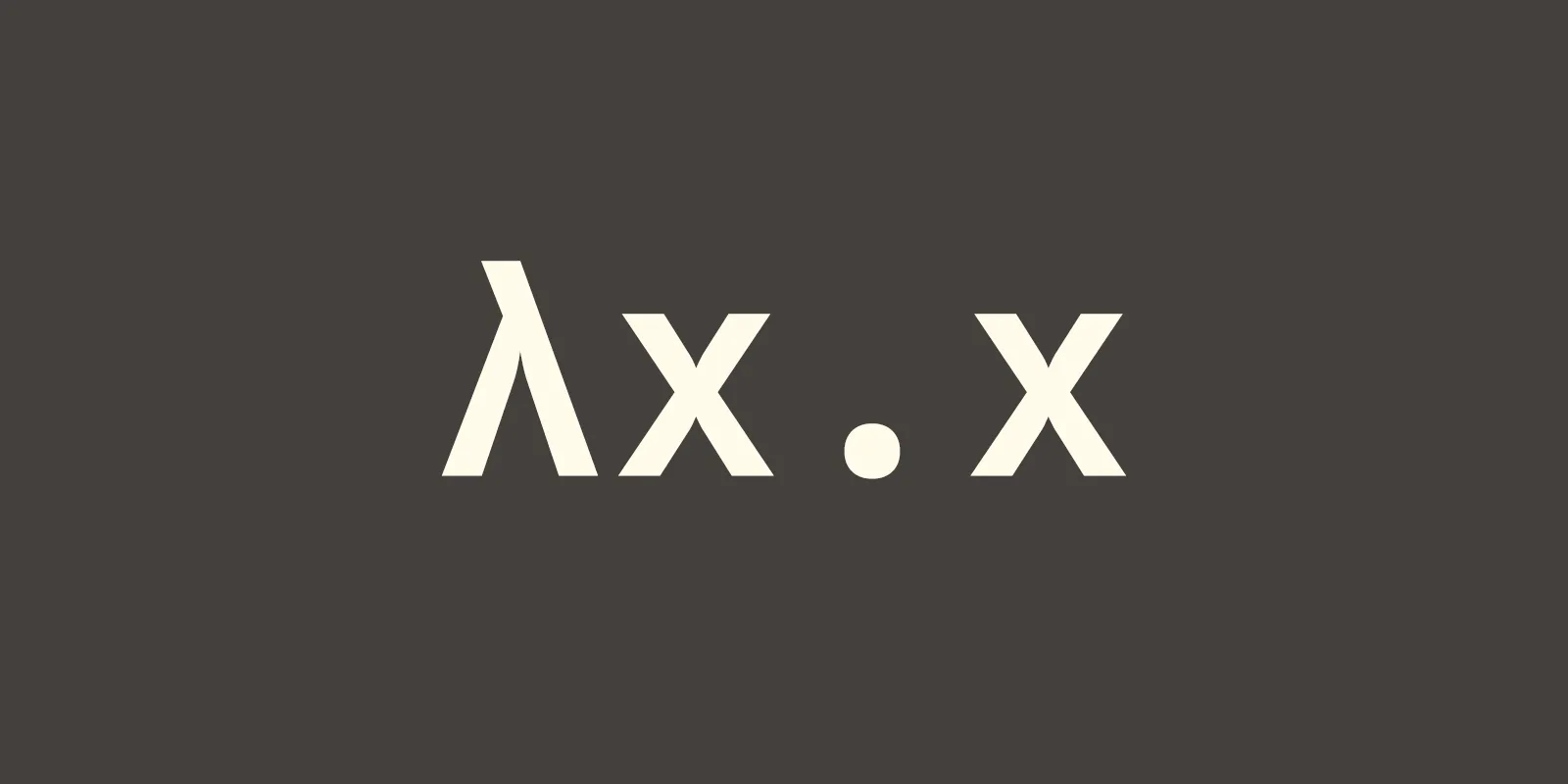Lambda Calculus: มีแค่ function ก็สร้างคอมพิวเตอร์ได้แล้ว

คำเตือน: แนะนำว่าถ้าไม่รู้จัก Turing Machine ให้ไปอ่านก่อนจะดีกว่า

ไอการที่มันจะเป็นคอมพิวเตอร์ที่เราใช้ ๆ กัน (หรือ programming language ส่วนใหญ่ที่เราใช้กัน) ได้เหนี่ย มันต้องเป็น Turing Complete ใช่ปะ? มันก็หมายความว่าถ้าเราคิดโมเดลบางอย่างขึ้นมาที่มันเป็น Turing Complete มาได้ มันก็พูดได้ว่ามันเป็นคอมพิวเตอร์แบบนึง (Kind of)

วันนี้ผมเลยอยากจะมานำเสนอโมเดลตัวนึงที่อาจจะพูดได้ว่าเป็น โมเดล Turing Complete ที่ simple ที่สุด ซึ่งทั้งโมเดลมันมีแค่อย่างเดียวก็คือ Function และสิ่งที่ผมจะมาเล่าวันนี้ก็คือ Lambda Calculus

disclaimer: โดยตัวบทความอันนี้จะเป็นเหมือนเรื่อง basic ที่ควรจะรู้กันใน Lambda Calculus เลยยังไม่ได้ลงรายละเอียดว่าทำไมมันถึงเป็น Turing Complete แต่ก็อาจจะอธิบาย concept ว่าทำไมมันทำได้

อะไรคือ Lambda Calculus?

อย่างแรกกี่ต้องบอกเลยก็คือ มันไม่ได้มีอะไรเกี่ยวข้องกับ Calculus ที่เราเรียน ๆ กันมานะ (ซึ่งน่าจะเป็นฝันร้ายของใครหลาย ๆ คน เลยอยากบอกก่อน กลัวปิดหนีไม่อ่านแล้ว 5555)

ถ้าให้พูดง่าย ๆ Lambda Calculus มันคือโมเดลทางคณิตศาตร์ตัวนึงที่คนเขาคิดมานี่แหละ

ซึ่งสิ่งที่มันพูดถึงเลยก็คือ ตัวมันจะมี funcion ที่หน้าตาแบบนี้

λx.y;

ซึ่งข้างบนเหนี่ยมันคือ function ใน Lambda Calculus ซึ่งมีความหมายว่า function ที่รับ x มา แล้วจะคืน y

การทำงานของ function ก็ปกติเลย

λx.xy

// (มองว่าแค่เอาของมาต่อกันก่อนละกัน)

(λx.xy)(z) = zy;

อืม ก็ไม่มีอะไรใช่ปะ นี่แหละความเจ๋งของ Lambda Calculus คือ ทั้งโมเดลมันมีแค่ไอนี่แหละ ไม่มีตัวเลข ไม่มีเครื่องหมายอะไรทั้งนั้น มีแค่ function หน้าตาแบบนี้

เห้ย มีแค่นี้แล้วมันจะไปทำอะไรได้ล่ะ? นี่แหละผมเลยอยากจะมาโชว์ให้ดูนิดหน่อยว่ามีแค่นี้มันก็ทำอะไรได้เยอะแยะ โดยผมจะค่อย ๆ แงะเป็นข้อ ๆ ตามนี้

1. Function มันก็คืนของออกมาเป็น function ได้นะ!

ในเมื่อเราได้เห็น function ที่ simple ที่สุดแล้วในโมเดล งั้นเรามาลองเขียนอะไรที่มันยากขึ้นนิดนึงละกัน

λx.λy.z;

โอเค เริ่มจากตัวนี้ คนอาจจะเริ่มงง ๆ ว่ามี λ สองตัวนี่มันคืออะไร ก็อย่างที่บอกไปข้างต้นว่า function มันคืน function อีกตัวมาได้ ซึ่งมันมีชื่อเรียกว่า higher-order function หรือ currying (ซึ่งเป็น concept ที่สำคัญอีกตัวนึงในโลก programming แนะนำให้ลองไปหาอ่านดู)

ซึ่งไอเจ้าข้างบนนี่มันคือแบบนั้นเลย โดยเรามองว่ามันคือ function ตัวนึงที่ รับของชื่อ x แล้วมันก็คืน function อีกตัวนึงที่รับ y แล้ว function นั้นมันจะคืน z อีกที

โอเค แล้วมันมีประโยชน์อะไรล่ะ? ถ้าให้พูดง่าย ๆ คือใน lambda calculus, function มันรับของได้แค่ตัวเดียว ดังนั้นถ้าเราอยากให้มันรับค่าได้หลายตัว ท่าที่ใช้ก็คือการทำแบบนี่นี่แหละ อย่างในตัวอย่าง เราก็สามารถพูดได้อีกแบบว่ามันคือ function ที่รับค่า x และ y แล้วจะคืน z ออกมานั่นเอง!

2. Function มันก็รับ function มาได้เหมือนกันนะ

โอเค เมื่อ function มันคืน function ได้ มันก็รับของเป็น function ได้ใช่ปะล่ะ

งั้นเริ่มจากตัวอย่างแรก โดยเราจะมี function ตัวนึงหน้าตาแบบนี้

i :: λx.x
// (ตัว :: มันคือการประกาศตัวแปรนั่นแหละ)

function ตัวแรกคือ λx.x ซึ่งบางคนอาจจะมองออกว่ามันคือ Identity Function โดยถ้าใครงง มันก็คือ function ที่ได้อะไรมาก็คืนตัวเดิมนั่นแหละ

ดังนั้นถ้าเรามี function อีกตัวนึงที่ชื่อ F แล้วเราใส่มันเข้าไปใน I ของที่ได้มาก็ต้อง F ตัวเดิมใช่ปะ?

f :: λx.y

// ดังนั้น
i(f) = (λx.x)(λx.y) = λx.y = f

โอเค ถ้าใครยังงง ๆ อยู่ เดี๋ยวจะอธิบายแบบนี้

เจ้า (λx.x)(λx.y) มันแบ่งเป็น 2 ส่วนตามวงเล็บ โดยวงเล็บแรกมันคือ function ที่ถูกใช้ ส่วนวงเล็บด้านหลังมันคือของที่ถูกใช้เป็น parameter ไปใส่แทน x มันเลยได้ตัวมันกลับมาเหมือนเดิม

โอเค งั้นต่อด้วยอะไรที่ซับซ้อนขึ้นละกัน

f :: λx.xx

g :: λx.xy

gf = (λx.xy)(f) =  fy = (λx.xx)(y) = yy

// fx มันคือเหมือน f(x) ที่เราเรียนกันมานั่นแหละ
// ในนี้วงเล็บใช้แค่บอกว่าจะทำอะไรก่อนกับจัด group เฉย ๆ

อันนี้ก็ไม่มีอะไร เราเอา f ไปแทนที่ x ใน function g แล้วพอ f มันเป็น function อยู่แล้ว ก็เลยยัด y เป็น parameter ให้ f ต่อ

3. มาลองทำ Boolean Algebra กันดีกว่า

โอเค ในเมื่อเรามีพื้นฐานระดับนึงแล้ว เรามาลองทำอะไรง่าย ๆ อย่าง Boolean Algebra กันเลย

สำหรับใครที่ไม่รู้จัก Boolean Algebra ง่าย ๆ มันก็คือพวก true false ที่ว่าจริงและจริงเป็นจริง จริงและเท็จเป็นเท็จ อะไรพวกนั้นนั่นแหละ

โดยใน Boolean Algebra ตัวพื้นฐานที่สำคัญ (และทำง่าย) จะมี 5 อย่าง ก็คือค่า true, false, not (เปลี่ยน true เป็น false, false เป็น true), and, และ or โดยถ้าเราทำของพวกนี้ได้ ก็สามารถทำของอย่างอื่นได้หมด

งั้นเริ่มจากการนิยาม true false ในระบบก่อนเลย ซึ่งในนี้เราจะนิยาม (มโนว่า)

true :: λx.λy.x (ได้ของ 2 ตัว คืนตัวแรก)

false :: λx.λy.y (ได้ของ 2 ตัว คืนตัวสอง)

// (นิยามที่เขียนมาในวงเล็บสำคัญมาก จำไว้ก่อน)

ในการนิยามอันนี้คือว่า ถ้าเราใส่ของอะไรเข้าไปใน function แล้วมันคืนของหน้าตาแบบนี้ออกมา ก็คือหมายถึงมันคืนค่า true, false เลย

โอเค เราได้ true, false แล้ว เรามาลองทำ function not ดีกว่า

not :: λx.(x)(false)(true)

// ถ้าเขียนแบบเต็มยศคือ
λx.(x)(λx.λy.y)(λx.λy.x)

ซึ่งอันนี้เรา abuse ความที่ว่าตัว boolean มันก็เป็น function อยู่แล้ว ดังนั้นถ้าเราใส่ true ไป ตัว true ตัวนั้นมันจะมองเป็น function ที่จะ คืนของตัวแรก มันเลยคืน false กลับมา

ในทางกลับกัน ถ้าเราให้ false ไป ตัว false มันก็จะทำหน้าที่เป็น function คืนค่าตัวที่สองกลับมา เราก็เลยได้ true กลับมานั่นเอง!

not(true) = ( λx.(x)(false)(true) )(true)
        = true(false)(true) # ยัด true แทน x
        = (λx.λy.x)(false)(true)
        = false # เอาตัวแรก

not(false) = ( λx.(x)(false)(true) )(false)
        = flase(false)(true) # ยัด false แทน x
        = (λx.λy.y)(false)(true)
        = true # เอาตัวสอง

งงไหม? ถ้างงก็ไม่แปลก ส่วนตัวก็ใช้เวลาสักพักเหมือนกัน แนะนำว่าทำความเข้าใจตัวนี้ให้ดี ๆ เพราะหลัง ๆ มันก็จะใช้หลักการประมาณนี้แหละ

โอเค พอเราได้ negate แล้ว พวก and, or ก็คงทำความเท่าใจไม่อยากแล้วแหละมั้ง โดยหน้าตาจะประมาณนี้

and :: λx.λy.x(y)(false);
// รับ boolean x y มา ถ้า x เป็น true มันจะคืนตัวแรกก็คือ y
// ถ้า y เป็น true ก็เป็น true เลย เป็น false ก็เป็น false เลย

// แต่ถ้า x เป็น false จะคืนตัวสองที่เป็น false ทันที

or :: λx.λy.x(true)(y);
// รับ boolean x y มา ถ้า x เป็น true มันจะคืนตัวแรกที่เป็น true ทันที

// แต่ถ้า x เป็น false จะคืนตัวสอง ซึ่งก็คือ y
// ถ้า y เป็น true ก็เป็น true เลย เป็น false ก็เป็น false เลย

4. มาลองทำจำนวนนับกันดีกว่า

ในเมื่อเรามี boolean แล้ว ก็ขยับขึ้นมาเป็นจำนวนนับกันดีกว่า

โดยจริง ๆ แล้ว การ represent จำนวนนับใน lambda calculus ก็ทำได้หลายแบบ แต่ที่ผมจะพูดคือตัวที่ “เข้าใจง่ายที่สุด” (ที่ก็จะแอบยากอยู่ดี 555) ซึ่งมันก็คือ Church encoding นั่นเอง

โดย concept ของ Church encoding มันจะประมาณว่า ให้ 0 คือ function ที่รับค่าเป็น function 2 ตัว (f และ x) โดย 0 จะคืนค่า x มาตรง ๆ แต่เลขต่อ ๆ ไป ก็จะเอา f มาครอบทับไปเรื่อย ๆ

0 :: λf.λx.x
1 :: λf.λx.f(x)
2 :: λf.λx.f(f(x))
3 :: λf.λx.f(f(f(x)))
...
easy!

ต่อมา เราก็มาพูดถึง function พื้นฐานตัวนึงเลยก็คือ function ที่หาค่าถัดไปของตัวเลข (จาก 0 ไปเป็น 1) โดยมันมีชื่อว่า Successcor

succ :: λn.λf.λx.f(n f x)
????

เริ่มดูงง ๆ แล้วใช่ปะ 5555 เอาจริง ๆ มันก็ไม่มีอะไรเลย แต่ว่าตัวการ group ของมันดูอ่านยากเฉย ๆ ลองมาทำให้มันเป็น function tsที่อ่านง่าย ๆ ดูดีกว่า

0 = (f,x) =>x

succ = (n: number, f, x) => f(n(f,x))

ก็คือจริง ๆ แล้ว มันก็แค่เอา f อีกตัวมาครอบนั่นแหละ แต่ด้วยความที่ว่า f กับ x ใน ตัวเลขมันจะเป็นอะไรก็ได้ ก็เลยต้อง pass มันเข้าไปด้วย